Les nombres complexes
Spécificités de DGPad
Quand les expressions et les fonctions sont arrivées dans DGPad, en 2014, chacun a pu réaliser que les calculs sur les nombres complexes étaient également implémentés.
Un article de MathemaTice a aussitôt été rédigé, et c'est Alain Busser qui s'est chargé d'illustrer la partie concernant les nombres complexes.
Depuis la programmation par blocs est arrivée dans DGPad ; alors cette page Scenari voudrait approfondir le sujet (merci Blockly), et parler en particulier du produit des nombres complexes, d'un point de vue autant algébrique que géométrique.
Attention : Pour expérimenter les calculs d'Alain ...
et pour la création de listes de points en général : quand on calcule les racines n-ièmes d'un point (en fait les racines de son affixe), le logiciel affiche les solutions sous forme de liste.
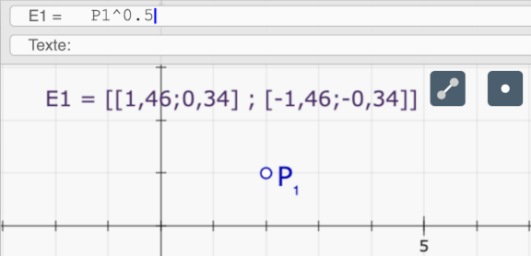
Pour transformer cette liste en liste de points, il suffit en principe de faire un clic sur le petit point en haut à droite. Mais il ne se passe rien ! En fait il y a un petit bug de raffraichissement. Pas de panique, un léger zoom/anti-zoom suffit pour la faire apparaître.
(pour plus d'informations sur les listes, on pourra consulter la page correspondante du didacticiel)
Objectif de ce module
Désormais les nombres complexes figurent au programme en terminale uniquement en « maths expertes ».On les trouve aussi en terminale STI2D.
L'idée ici développée : introduire ce chapitre directement à partir de deux figures DGPad :
La première permet de définir le produit de nombres complexes
La seconde parle de distributivité de l'addition par rapport à la multiplication.
Les prérequis (pour les élèves)
Ils sont réduits au minimum :
la somme de deux vecteurs
la définition des coordonnées polaires (uniquement la définition, aucune expertise à ce sujet)
la définition d'une rotation (uniquement la définition, aucune expertise à ce sujet)
la définition d'une homothétie, et l'image d'un couple de points dans une homothétie
Remarque :
L'idée ici proposée : partir directement des figures pour introduire la notion de nombre complexe. Mais il est possible de procéder différemment : utiliser les deux figures après avoir dévelloppé son cours ; afin de proposer des images mentales un peu parlantes.
1- L'opération +
Si \(A\) et \(B\) sont deux points déjà existants la calculatrice DGPad permet l'entrée \(A+B\).
Une validation directe renvoie la liste de la somme des coordonnées.
Mais un clic sur l'icône « point » en haut à droite renvoie le point \(C\) défini par \(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}\).
L'addition des points, ça n'existe pas ! En réalité c'est un raccourci commode pour calculer la somme de leurs coordonnées.
2- L'opération A*...
Ajouter des points c'est possible dans DGPad. Mais les multiplier aussi. Là encore c'est une liste (ou un point) qui sont obtenus, avec une définition à priori un peu mystérieuse.
La figure ci-dessous va permettre d'élucider le mystère. La clé ? Passer aux coordonnées polaires.
Remarque :
Il vaut mieux utiliser la figure en mode « consultation » (petite flèche à gauche non sélectionnée)
Les points A et B sont aimantés par l'axe horizontal, l'axe vertical, les points I et J, ainsi que le cercle unité.
Étude de l'opérateur A*... sur le point B
Quelques grandes lignes sur ce que peut inspirer l'analyse de cette figure.
Au niveau algébrique, il semble bien que la règle soit la suivante : on multiplie les rayons (désormais appelés modules) et on ajoute les angles (désormais appelés arguments). Conséquence : l'opération * est commutative.
L'axe horizontal c'est l'axes des réels, qui est plongé dans le plan de ces nouveaux nombres. Quand \(A\) et \(B\) sont sur l'axe horizontal (mode coordonnées cartésiennes), donc des réels (la deuxième coordonnée disparaît, c'est voulu). Alors l'opération * .. c'est tout simplement le produit ordinaire. D'où l'idée de garder le nom produit, même lorsque A et B sont quelconques.
Si \(A\) est placé en J, observer et conclure. Si \(A\) et \(B\) sont placés en \(J\) : \(J*J=-1\) !
Question : \(A\) est placé sur l'axe des réels, \(B\) est quelconque. Quelle transformation fait passer de \(B\) à \(A*B\) ? Pour mieux visualiser, \(B\) est un point de l'image « Rantanplan », et la transformation concerne aussi « Rantanplan » (il vaut mieux le mode coordonnées polaires).
Cette fois \(A\) est placé sur le cercle unité (mode coordonnées polaires). Mêmes questions.
Après être passé en mode création, créer une demi-droite d'origine O puis aimanter \(A\) par cette demi-droite. Le passage de \(B\) à \(A*B\) est une rotation de centre \(O\) et d'angle l'argument de \(A\), suivie d'une homothétie de centre \(O\) et de rapport le module de \(A\).
3- Distributivité de l'opération * par rapport à l'addition
Un peu de géométrie
Un très rapide cours sur les transformations précédentes (qui ne sont plus au programme). Mais qui suffit pour comprendre la suite.
Les rotations :
ce sont des isométries (Al-Kashi ...)
donc elles conservent les milieux (caractérisation du milieu)
donc elles transforment un parallélogramme en un parallélogramme.
Les homothéties :
Un vecteur \(\overrightarrow{AB}\) est transformé en \(k \overrightarrow{AB}\)
donc un parallélogramme est transformé en un parallélogramme.
Addition et multiplication
C'est la figure ci-dessus qui est utilisée.
Le quadrilatère rose est un parallélogramme : il a été obtenu en entrant \(B+C\) dans la calculatrice.
Il y a deux méthodes pour obtenir le sommet non nommé du parallélogramme gris :
soit entrer \(A*B+A*C\) dans la calculatrice (attention il faut choisir les points à la souris et nom entrer leurs noms directement)
soit entrer \(A*(B+C)\) puisque l'image d'un parallélogramme par une rotation suivie d'une homothétie est un parallélogramme.
Il y a bien distributivité de l'addition par rapport à la multiplication.
Les notations définitives
Dans ce qui précède on n'hésite pas à ajouter des points et à les mutiplier ! Mais il faut bien avoir à l'esprit que ce ne sont que des raccourcis. En réalité sous chaque point du plan se trouve un « nouveau nombre » (un nombre complexe) appelé affixe de ce point ; et ce sont les affixes qui sont ajoutées ou multipliées. L'affixe d'un point \(A\) se note \(z_A\), et la multiplication se note comme pour les réels : ce qui est cohérent puisque pour les réels on a vu que l'opération * coïncide avec la multiplication connue.
L'affixe du point J se note \(i\). Ainsi \(i\times i=-1\), ce qui s'écrit aussi \(i^2=-1\)
L'affixe d'un point peut être le couple \((x,y)\) de ses coordonnées cartésiennes. Désormais on pourra l'écrire \((x,0)+i\times (y,0)\) ou plus simplement \(x+iy\) : tout à fait justifié puisque le produit par \(i\) fait subir une rotation de centre O et d'angle 90° et que l'ensemble des réels est « plongé » dans l'ensemble des complexes ;
Elle peut être aussi le couple de ses coordonnées polaires \((r,\theta)\). Désormais on lui préfèrera la notation \(re^{i\vartheta}\). Que vient faire l'exponentielle là dedans ? pour l'instant ce n'est qu'une notation justifiée par le fait que la multiplication de complexes multiplie les modules et ajoute les arguments : \((r,\theta)*(r',\theta')=(r\times r',\theta + \theta')\) ; de même que : \(re^{i\theta}\times r'e^{i\theta'}=r\times r'e^{i(\theta + \theta')}\)
Un petit calcul à effectuer : \((x+iy)(x'+iy')\). Et vérifier sur des exemples dans la toute première figure que cela correspond bien à l'opérateur * quand on choisit les coordonnées cartésiennes.
4- Suites de nombres complexes
Dans le programme officiel de maths expertes on propose : « Étude expérimentale de l’ensemble de Mandelbrot ».
Ce qui est proposé ici c'est beaucoup plus simplement la programmation de la suite des nombres complexes définie par récurrence par :
\(z_{n+1}=z_{n}^2+c\) (et ici \(z_0\) quelconque)
Mais c'est aux élèves q'il est demandé de programmer eux-mêmes de telles suites ... en Blockly.
Première figure
La suite demandée (avec 2000 points) est déjà construite. Mais c'est une boîte noire : le secret de sa programmation est super-caché. On peut cependant expérimenter ce qui se passe quand c varie.
Le travail demandé : effectuer un clic sur \(liste\), puis sur l'icône « puzzle »
S'ouvre alors la fenêtre Blockly \(DG-Blocks :liste\) qu'il suffit de compléter.

Remarque :
Le Blockly de DGPad permet, comme le logiciel lui-même, la somme des points (plus précisément de leurs affixes) ainsi que leur produit. C'est ce qui a été utilisé dans la création de la fonction f, qui est donc une fonction définie sur l'ensemble des nombres complexes.
Le complexe \(i\) figure dans l'onglet \(Math\) (mais n'est pas utilisé ici).
Seconde figure
Même type de question, mais cette fois sans utiliser de fonction : le calcul de l'image se fait directement dans la boucle.