Curvica ... triangulaire !
Curvica est un puzzle pédagogique de 24 pièces inventé par Jean Fromentin en 1982, publié par l’APMEP et également richement développé par l’IREM de la Réunion.
Yves Martin (IREM de la Réunion) en a donné une version en ligne, fabriquée avec le logiciel DGPad : les pièces sont construites en utilisant des macros-constructions.
Alors pourquoi une nouvelle page à ce sujet déjà si largement et joliment développé ?
pour plus de simplicité (certains l'ont déjà fait) les pièces ne sont plus à base carrée mais sont à base triangulaire (le jeu s'appellera dorénavant Curvitri)
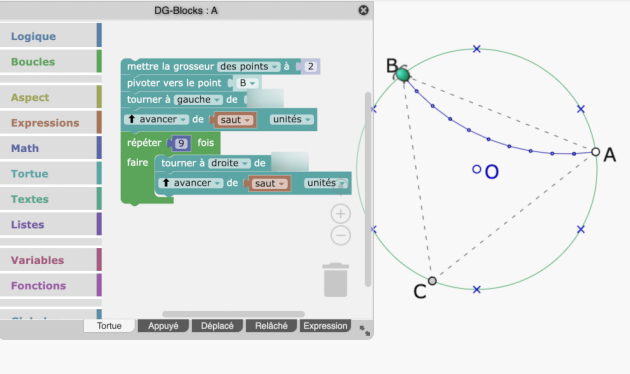
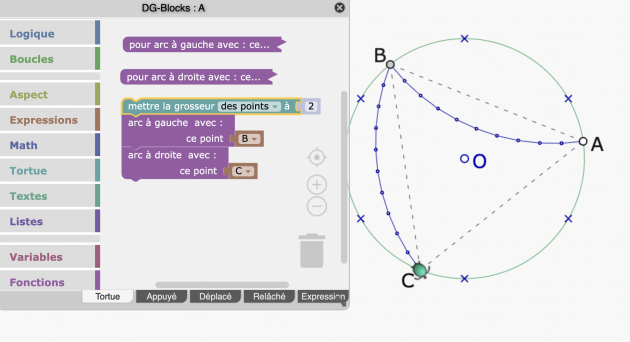
dans notre version en ligne, l'intérieur des pièces est colorié ; ce qui est impossible si on les construit avec des macros combinant arcs de cercle et segments juxtaposés ; mais qui devient possible si elles le sont en Blockly (mode tortue). C'est le but véritable de cette page : donner un exemple illustré de programmation par blocs à l'intérieur d'un logiciel de géométrie dynamique.
1- Le jeu pour les plus jeunes
Règle du jeu :
Déplacer les onze pièces dans le tableau à double entrée ci-dessous, de manière à les ranger à la fois selon leur aire et leur périmètre.
2- les puzzles
2-a Le plateau de jeu
Assembler les pièces du curviTri sur le tableau gris aimanté pour former librement de jolies figures ; ou reconstituer les figures imposées du paragraphe suivant.
Note : il y a une double aimantation, celle du centre de la pièce pour leur translation et celle des croix vertes qui permettent leur rotation.
2-b Les modèles à reproduire
Un disque, un hexagone, un trapèze et une jolie forme symétrique.
Prolongement : trouver d'autres jolies formes ...
3- Pour les plus grands : du Blockly !
Les « arcs de cercle » utilisés pour la construction des pièces du Curvitri sont en fait des lignes polygonales. L'intérêt ? L'intérieur d'une ligne polygonale fermée peut être « rempli » (de couleur).
La construction de telles lignes est ici proposée sous forme d'exercice.
3.a Les calculs préliminaires
À vos crayons ! Quelques calculs trigonométriques simples (niveau classe de troisième) permettent de démarrer l'activité.
Toutes nos pièces du Curvitri ont pour base un triangle équilatéral inscrit dans un cercle de rayon 2 ; certains des côtés sont remplacés par un faux arc de cercle de 60° : en fait une ligne polygonale régulière à 10 côtés (voir la figure ci-dessous ... une simple image)
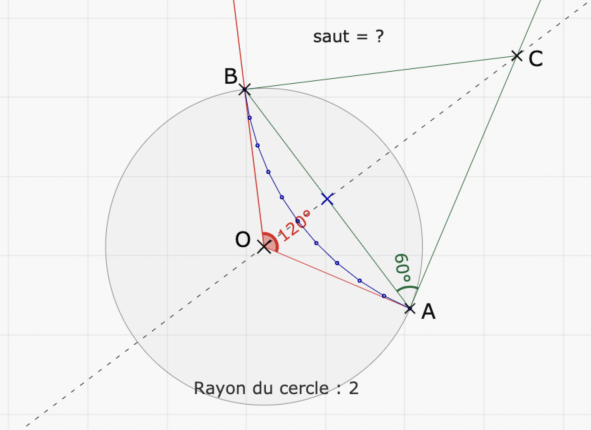
Il vous faudra calculer (si on imagine que la ligne polygonale s'appelle AA1A2A3A4....B) :
la distance AA1 (appelée « saut » dans la suite)
l'angle BAA1 (pour faire tourner la tortue la première fois)
l'angle AA1A2 (pour faire tourner la tortue les fois suivantes)
3.b Les modèles inspirants
Première capture d'écran (pour le paragraphe 4) : les valeurs des angles à utiliser ont été cachées ... et c'est voulu.
Seconde capture d'écran : les blocs de la figure précédente ont été inclus dans une fonction « arc à gauche »
Une fonction « arc à droite » a été ajoutée.
3.c À vous de jouer
Il est conseillé d'ouvrir la figure en plein écran, ou mieux encore de la télécharger si l'appli locale est installée.
La première chose à faire : créer dans la figure une expression (appelée « saut », en lui donnant la valeur exacte du calcul effectué plus haut.
Ensuite : placer une tortue en A ... et la faire avancer sur le pseudo arc de cercle en 10 petits sauts.
Remarque :
Le point A, libre sur le cercle, est aimanté par les 6 autres points en forme de croix.
La construction du cercle de rayon 2 accompagné de ses 3+6 points a été transformée en macro : en appliquant ladite macro plusieurs fois vous pourrez construire plusieurs bases de pièces du curvitri : ne pas oublier qu'il est ensuite possible de copier (par clic-droit) les blocs ou groupe de blocs d'un DG-Block à un autre.
3.c Les secrets de la grille !
C'est tout simplement une liste de points !
Un clic sur l'expression « a » puis le choix de l'icône « bloc » vous donne le secret du double balayage utilisé.
Une grille peut être aimantée ! Ici elle attire à 10 pixels tous les centres de toutes les pièces de notre Curvitri
Dernier secret : la figure avec toutes les pièces du curvitri et celle avec la grille ont été faites séparément. Puis avec un « copier la figure » suivi d'un « coller la figure » la première a été ajoutée à l'autre ! Merci au développeur d'avoir implémenté cette jolie fonctionnalité.