Didacticiel DGPad

Quand on effectue un "tap" sur un objet, on obtient la palette ci-dessous, avec moins d'icônes parfois : tout dépend du contexte !

DGPad est conçu d'abord pour tablette, et l'auteur voulait à tout prix la prévisualisation des constructions. Alors il a fallu imaginer quelque chose de différent de ce qui se passe sur PC. La raison est très simple : si la main lâche la souris, le pointeur reste toujours visible à l'écran, tandis que sur tablette, après avoir levé le doigt, il n'y a aucun moyen de retrouver la dernière position de ce doigt pour continuer la construction. Le choix qui a été fait par souci de simplicité, même si d'autres choix étaient tout à fait envisageables : un seul doigt, mais maintenu posé pour ensuite glisser. C'est naturel sur tablette, mais il faut se forcer un peu pour faire la même chose avec la souris !

Une petite vidéo vaut mieux qu'un long texte d'explications ...

Une fois qu'on a compris ceci, chaque outil devient très simple d'utilisation et ne nécessite pas un mode d'emploi individuel. Sauf pour trois d'entre eux : l'outil cercle de mesure imposée, l'outil angle et l'outil angle de mesure imposée (ceux qui sont entourés de rouge) . Leur utilisation est également très simple, mais si on veut profiter de toutes les subtilités les concernant (degrés ou radians ? orientés ou non orientés ?) il est nécessaire d'apporter des précisions. Ce qui est fait dans les trois paragraphes suivants.

Il suffit d'une courte vidéo pour comprendre.

• Remarque 1 : si on est en mode degrés par exemple on peut quand même basculer la calculatrice en mode radians pour un calcul indépendant de la figure (qui peut alors se trouver quelque peu chamboulée). Et bien évidemment, le calcul terminé, on la repassera aussitôt en mode degrés.

• Remarque 2: si on est en mode radians ne pas s'étonner si les angles affichés ... restent en degrés ! Dans ce cas ce sont les calculs effectués à partir des angles de la figure qui utilisent les radians.

• Remarque 3 : des macros rotations (voir détails au paragraphe 3) sont maintenant disponibles. Celle « avec dialogue » qui demande des degrés ne fonctionne que ... pour les figures en mode degrés ! Si la figure est en mode radians (lycée ou supérieur) on traitera les rotations par les nombres complexes, et on se fera éventuellement ses propres macros.

• Remarque 4 : les figures 3D sont par défaut en mode radians (il est possible d'en changer).

• Remarque 5 : si on l'intention d'utiliser la tortue, il faut rester en mode radians.

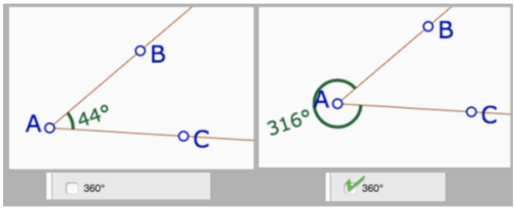
Tout angle créé est par défaut géométrique, c'est à dire un angle non orienté de demi-droites (ici dans l'ordre on a montré B, puis A puis C). Mais par l'intermédiaire du panneau de propriétés il est possible de le transformer en angle orienté de vecteurs ; avec une remarque très importante : la mesure principale affichée est dans l'intervalle [0° ; 360°] (habitude anglo-saxonne ?'allemande ?) et non pas comme dans la plupart des manuels français dans l'intervalle [-180°;180°].

Il permet en engagement direct de construire un angle qu'on s'est choisi. Par défaut c'est une mesure affichée en degrés (nombre entier) comprise entre 0° et 180° (l'angle est géométrique).

Mais comme tous les objets construits, si on utilise la calculatrice pour inspecter l'angle en question il est possible d'entrer un nombre décimal, ou un nombre dépassant 180°, ou encore une expression déjà définie.

L'angle une fois construit, par le panneau de propriétés on peut en « changer le sens ».